在上一篇文章中，我们已经实现了点绘制的功能。基于点绘制的功能，我们使用 Bresenham 画线算法，实现了画线功能。

这篇文章中，我们实现三角形绘制的功能。分为两大部分讲解：第一部分介绍并实现向量运算；第二部分基于实现的向量运算，完成三角形绘制功能。

1. 向量运算

向量上的运算包括向量的加法、减法、标量乘法等，这些就不做介绍了。此处说明一下点积和叉积，这两个概念在向量运算相关的书籍上，也都是老生常谈的篇幅了。但是自己接触下来还是很陌生，所以这边以我自己提问题的形式，对相关概念进行说明。

Q1: 几何公式和向量公式的等价

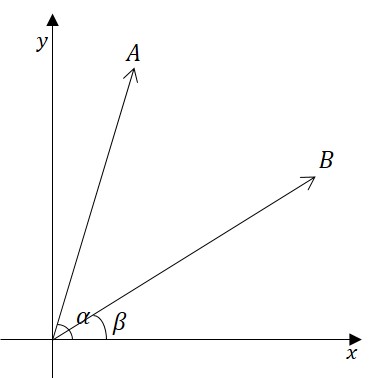
如图 1 所示，说明叉积的公式推导。主要就是用到三角函数的和差公式。

\(\vec{A}\times\vec{B}=\lvert \vec{A} \rvert \lvert \vec{B} \rvert \text{sin}(\theta)=\lvert \vec{A} \rvert \lvert \vec{B} \rvert \text{sin}(\alpha - \beta) \)

\(=\lvert \vec{A} \rvert \lvert \vec{B} \rvert \{\text{sin}(\alpha)\text{cos}(\beta)-\text{cos}(\alpha)\text{sin}(\beta)\} \)

\(=\lvert \vec{A} \rvert \text{sin}(\alpha) \lvert \vec{B} \rvert \text{cos}(\beta) - \lvert \vec{A} \rvert \text{cos}(\alpha) \lvert \vec{B} \rvert \text{sin}(\beta) \)

\(=B_x A_y - B_y A_x\)

在上面式子中，可以发现结果和向量公式的结果是相反数。如果在图中交换向量 \(A\) 和 \(B\) 的位置，就能和向量公式一样。一样的思路推导，可以发现点积结果是无关顺序的。这是叉积有方向的一个直观体现。

Q2: 叉积的方向和右手定则

叉积的方向垂直于两个向量所在的平面，这是三维上的概念。所以，我们先把二维的叉积统一梳理到三维上。

用行列式的概念，方便说明。三维叉积：

\(\begin{vmatrix} i & j & k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}\)

二维的话 \(z\) 轴坐标为 0，展开的话，结果其实就是 \(z\) 轴上的分量：

\(\begin{vmatrix} i & j & k \\ a_x & a_y & 0 \\ b_x & b_y & 0 \end{vmatrix}=k\begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix}\)

接着，我们顺便证明一下叉积是垂直于向量所在平面的。我们把叉积结果和各个向量做点积，看结果是否为 0。我们先看 \((a_x,a_y,a_z)\)：

\(a_x \begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} + a_y \begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix} + a_z \begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix} \)

\(=\begin{vmatrix} a_x & a_y & a_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix}=0\)

可以直接看成 \((a_x,a_y,a_z)\) 按行展开。行列式两行相同，结果为 0。同理另一个向量也是，所以叉积的方向垂直于两个向量所在的平面。

现在我们回到右手定则的讨论上。我们已知叉积都是垂直两个向量所在的平面，它“朝里”还是“朝外”是由 \(z\) 轴上分量决定的。

即 \(\begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix}\) 的正负决定的。

看到 Q1 中的几何公式，要判断正负性，其实就是判断两个向量之间的角度。右手定则就是判断角度用的。

2. 向量运算代码实现

对应的实现，记录在 tag/vector_ops。

实现的思路是，如代码清单 2.1 所示，用模板定义一个向量的基类 Vector，在上面实现各种通用的操作：加法、减法、标量乘法、标量除法。

1. template<typename T, size_t N>
2. class Vector
3. {
4. protected:
5.     T elements[N];
6.  
7. public:
8.     Vector()
9.     {
10.     }
11.  
12.     Vector(std::initializer_list<T> init)
13.     {
14.         assert(init.size() == N);
15.         size_t i = 0;
16.         for (auto& e : init)
17.             elements[i++] = e;
18.     }
19.  
20.     size_t size() const
21.     {
22.         return N;
23.     }
24.  
25.     Vector& operator=(const Vector& rhs)
26.     {
27.         if (this != &rhs)
28.             memcpy(elements, rhs.elements, N * sizeof(T));
29.         return *this;
30.     }
31.  
32.     T& operator[](size_t i)
33.     {
34.         assert(i < N);
35.         return elements[i];
36.     }
37.  
38.     const T& operator[](size_t i) const
39.     {
40.         assert(i < N);
41.         return elements[i];
42.     }
43.  
44.     Vector operator+(const Vector& rhs) const
45.     {
46.         Vector res;
47.         for (size_t i = 0; i < N; i++)
48.             res[i] = elements[i] + rhs.elements[i];
49.         return res;
50.     }
51.     // …… ……
52.     // …… ……
53. }

对于二维向量，继承上述实现的 Vector 类。再在上面添加特定的函数，如代码清单 2.2 所示，我们通常会以 .x()、.y() 方式访问分量，命名更加直观。三维向量也是如此。

1. template<typename T>
2. class Vector2 : public Vector<T, 2>
3. {
4. public:
5.     Vector2()
6.     {
7.     }
8.  
9.     Vector2(T x, T y) : Vector<T, 2>({ x, y })
10.     {
11.     }
12.  
13.     T& x() { return Vector<T, 2>::elements[0]; }
14.     T& y() { return Vector<T, 2>::elements[1]; }
15.  
16.     const T& x() const { return Vector<T, 2>::elements[0]; }
17.     const T& y() const { return Vector<T, 2>::elements[1]; }
18. };

对于点积和叉积，如代码清单 2.3 所示，写成全局函数的方式，调用的形式看着更加舒服。

1. template<typename T, size_t N>
2. T dot(const Vector<T, N>& a, const Vector<T, N>& b)
3. {
4.     T sum = 0;
5.     for (size_t i = 0; i < a.size(); i++)
6.         sum += a[i] * b[i];
7.     return sum;
8. }
9.  
10. template<typename T>
11. T cross(const Vector<T, 2>& a, const Vector<T, 2>& b)
12. {
13.     return a[0] * b[1] - a[1] * b[0];
14. }

3. 三角形绘制原理

前两节介绍了向量并且用代码实现了向量计算。现在我们来看到底怎么运用它，有什么实际的应用场景。

三角形扫描绘制算法

这边的三角形绘制不是只画三条线，而是指三角形的像素绘制。所以我们需要解决如何确定三角形所覆盖的像素。步骤为：

1. 确定扫描区域。如图 2 所示，我们选用三角形顶点最小和最大的 x、y 坐标，必然是包括三角形所在区域的。

2. 扫描遍历每个像素，检查它是否位于三角形内部。

3. 在三角形内部的像素进行着色。

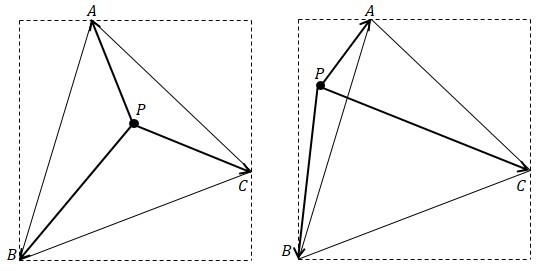
如何判断某个点是否在三角形区域内，我们可以计算 \(\overrightarrow{PA}\times\overrightarrow{PB}\)、\(\overrightarrow{PB}\times\overrightarrow{PB}\)、\(\overrightarrow{PB}\times\overrightarrow{PA}\) 的值。如果值符号都一致，则在三角形内，否则就在三角形外。

用叉乘进行检测很好解释，在上一节中我们已经了解到叉乘的正负性就是对应的角度。三角形的内角小于 180 度，所以无论顺时针遍历各个向量，还是逆时针，如果点在三角形内，扫过的角都是内角；而在三角形外，就会出现大于 180 的情况。

三角形重心插值算法

我们已经解决像素点的问题了，现在我们解决着色问题：我们只指定了三角形三个顶点的颜色，三角形内部点的颜色怎么渐变合理。

可以使用三角形重心插值算法算出针对点的权重，然后将这个权重作用到颜色上。三角形重心插值可以这么推导，我们将 \(\overrightarrow{AP}\) 用 \(\overrightarrow{AB}\) 和 \(\overrightarrow{AC}\) 表示，即换一个坐标系表示。

\(\overrightarrow{AP}=a \overrightarrow{AB} + b \overrightarrow{AC}\)，

\(P=(1-a-b)A+aB+bC\)

我们可以重新整理成书籍上给出的形式：

\(P=\alpha A + \beta B + \gamma C\)，其中 \(\alpha + \beta + \gamma = 1\)

求两个变量，x 和 y 分量对应两条方程，可以直接算出各个系数的值。

我们手算出的值，会发现是叉乘的形式。二维叉乘的几何意义对应三角形的面积（的一半）。转化成几何意义，我们会发现

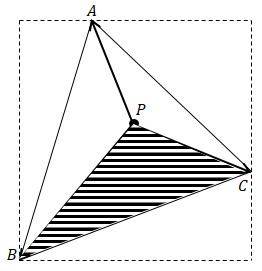
\(\alpha = \frac{S_{\text{PBC}}}{S_{\text{ABC}}}\)

\(\beta\) 和 \(\gamma\) 类似，都是顶点对应边和 P 点组成的小三角形和大三角形的比值。如图 3 所示，这是符合直觉的，P 点离 A 点越近，A 的权重就越大，组成的小三角形 PBC 面积就越大；而且三个小三角形加起来的面积就是大三角形的面积（\(\alpha + \beta + \gamma = 1\)）。

4. 三角形绘制的代码实现

最后，我们实现三角形绘制的代码。对应的完整实现，记录在 tag/draw_triangle。

如代码清单 4.1 所示，第 4 至 7 行计算三角形覆盖范围，然后按照这个范围进行遍历。area 变量是三角形 ABC 的面积。接着第 20 至 26 行计算三个叉积，以此判断点是否在三角形内部。这三个叉积可以“复用”，正好可以用来算三角形面积，从而得到三角形重心的权重（第 31 行）。

1. void TRasterizer::DrawTriangle(const tmath::Point2i& p1, const tmath::Point2i& p2, const tmath::Point2i& p3,
2.     TRGB888 color1, TRGB888 color2, TRGB888 color3)
3. {
4.     int minX = std::min(p1.x(), std::min(p2.x(), p3.x()));
5.     int maxX = std::max(p1.x(), std::max(p2.x(), p3.x()));
6.     int minY = std::min(p1.y(), std::min(p2.y(), p3.y()));
7.     int maxY = std::max(p1.y(), std::max(p2.y(), p3.y()));
8.  
9.     tmath::Vec2i p, pp1, pp2, pp3;
10.     int c1, c2, c3;
11.     float area = (float)std::abs(tmath::cross(p2 - p1, p3 - p1));
12.  
13.     for (int i = minX; i <= maxX; i++)
14.     {
15.         p.x() = i;
16.         for (int j = minY; j <= maxY; j++)
17.         {
18.             p.y() = j;
19.  
20.             pp1.x() = p1.x() - p.x(); pp1.y() = p1.y() - p.y(); // pp1 = p1 - p;
21.             pp2.x() = p2.x() - p.x(); pp2.y() = p2.y() - p.y(); // pp2 = p2 - p;
22.             pp3.x() = p3.x() - p.x(); pp3.y() = p3.y() - p.y(); // pp3 = p3 - p;
23.  
24.             c1 = tmath::cross(pp1, pp2);
25.             c2 = tmath::cross(pp2, pp3);
26.             c3 = tmath::cross(pp3, pp1);
27.  
28.             if ((c1 > 0 && c2 > 0 && c3 > 0) ||
29.                 (c1 < 0 && c2 < 0 && c3 < 0))
30.             {
31.                 TRGB888 color = TRGB888::Interpolate(
32.                     color1, std::abs(c2) / area,
33.                     color2, std::abs(c3) / area,
34.                     color3, std::abs(c1) / area);
35.                 SetPixel(i, j, color);
36.             }
37.         }
38.     }
39. }

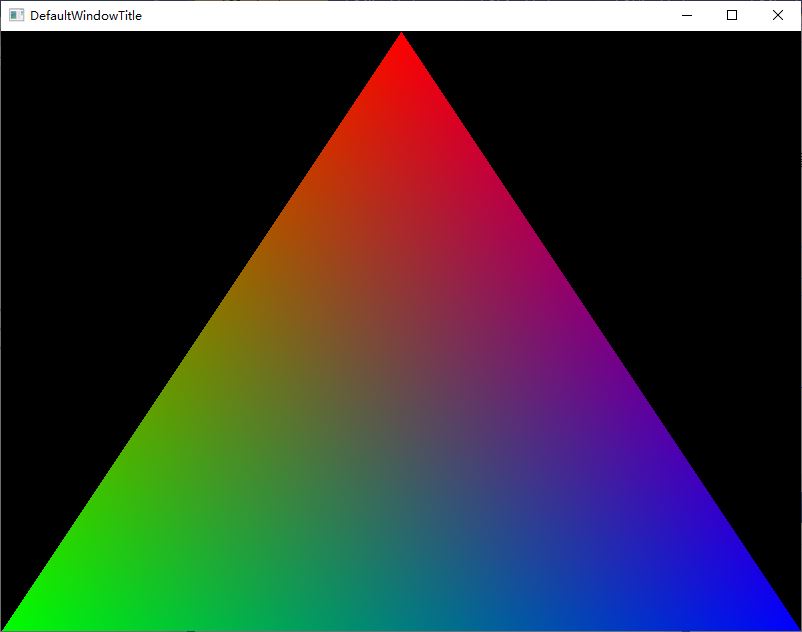
代码清单 4.2 是测试代码，三角形的三个顶点分别设置为红绿蓝。最终的效果如图 4 所示。

1. void TColorfulTriangleRenderTask::Render(TRasterizer& rz)
2. {
3.     int centerX = rz.GetWidth() / 2;
4.     int centerY = rz.GetHeight() / 2;
5.  
6.     rz.Clear(TRGB888(0, 0, 0));
7.  
8.     rz.DrawTriangle({ centerX, 0 }, { 0, rz.GetHeight() }, { rz.GetWidth(), rz.GetHeight() },
9.         TRGB888(255, 0, 0), TRGB888(0, 255, 0), TRGB888(0, 0, 255));
10. }