本章将深入探讨扩散模型背后的理论，并了解其内部工作原理。神经网络模型是如何生成如此逼真的图像的？好奇的我们希望揭开其神秘面纱，一窥其内部运作。

我们将触及扩散模型的基础，旨在弄清其内部工作机制，并为下一章实现可用的流程奠定基础。

通过理解扩散模型的复杂性，我们不仅可以加深对高级稳定扩散模型（也称为潜变量扩散模型，LDM）的理解，还能更有效地浏览 Diffusers 包的源代码。

这种知识将使我们能够根据新兴需求扩展该包的功能。

具体来说，我们将探讨以下主题：

• 理解图像到噪声的过程

• 更高效的前向扩散过程

• 噪声到图像的训练过程

• 噪声到图像的采样过程

• 理解分类器引导去噪过程

到本章结束时，我们将深入了解由 Jonathan Ho 等人提出的扩散模型的内部工作原理。我们将理解扩散模型的基本思想，并学习前向扩散过程。同时，我们还将掌握用于扩散模型训练和采样的反向扩散过程，并学习如何实现文本引导的扩散模型。

让我们开始吧。

理解图像到噪声的过程

扩散模型的思想来源于热力学中的扩散概念。将一幅图像比作一杯水，向图像（水）中加入足够的噪声（墨水），最终将图像（水）变成完全的噪声图像（墨水水）。

如图 4.1 所示，图像 x_0 可以被转换为近似高斯分布（正态分布）的噪声图像 x_t。

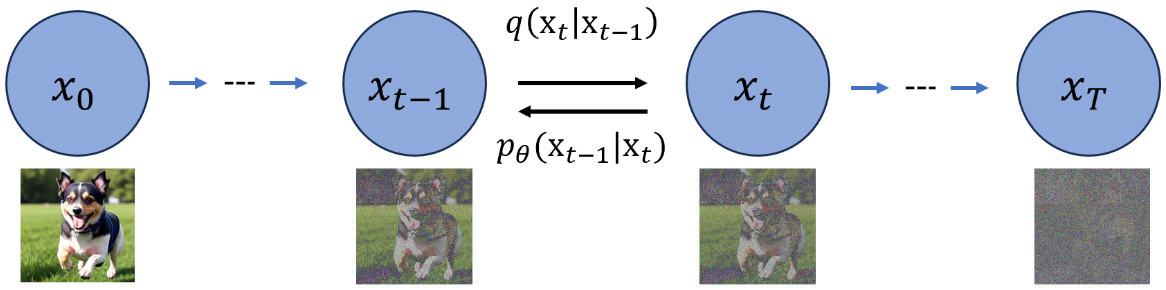
我们采用一个预定义的正向扩散过程，用 q 表示，该过程系统性地向图像中引入高斯噪声，直到最终成为纯噪声。该过程记为 q(x_t \mid x_{t-1})。需要注意的是，反向过程 p_\theta(x_{t-1} \mid x_t) 仍然未知。

正向扩散过程的一步可以表示如下：

q(x_t \mid x_{t-1}) := \mathcal{N}(x_t; \sqrt{1-\beta_t} \, x_{t-1}, \beta_t \mathbf{I})

让我从左到右逐步解释这个公式：

• 符号 q(x_t \mid x_{t-1}) 表示一个条件概率分布。在这种情况下，分布 q 表示在给定前一步图像 x_{t-1} 的条件下，观察到噪声图像 x_t 的概率。

• 公式中使用定义符号 := 而不是波浪符号 \sim，因为正向扩散过程是一个确定性过程。波浪符号 \sim 通常用于表示一个分布。如果在此使用波浪符号，公式的含义将是噪声图像是一个完整的高斯分布。然而，实际情况并非如此。在第 t 步，噪声图像由前一步图像和添加的噪声的确定性函数定义。

• 那么为什么这里使用 \mathcal{N} 呢？符号 \mathcal{N} 用于表示高斯分布。然而在这种情况下，\mathcal{N} 是用来表示噪声图像的函数形式。

• 在右侧，分号之前的 x_t 是我们希望服从正态分布的量；分号之后的是分布的参数。分号通常用于分隔输出和参数。

• \beta_t 是第 t 步的噪声方差，\sqrt{1-\beta_t} \, x_{t-1} 是新分布的均值。

• 为什么公式中使用大写 \mathbf{I}？因为一个 RGB 图像可能有多个通道，单位矩阵可以独立地将噪声方差应用于不同的通道。

用 Python 向图像添加高斯噪声非常简单：

图像以网格形式绘制，如图 2 所示。

从结果可以看出，尽管每一幅图像都来自一个正态分布函数，但并非每一幅图像都是一个完全的高斯分布，更严格来说，并非一个各向同性高斯分布。只有在将步数设为无限大时，图像才会成为一个完全的高斯分布。但这并不必要。在原始的 DDPM 论文中，步数被设定为 1000，而在后来的 Stable Diffusion 中，步数减少到 20 至 50 之间。

如果图 2 的最后一张图像是一个各向同性高斯分布，其二维分布的可视化将呈现为一个圆形；其特点是所有维度上的方差相等。换句话说，分布的扩展或宽度在所有轴上是相同的。

让我们绘制添加了 16 倍高斯噪声后的图像像素分布：

结果如图 3 所示。

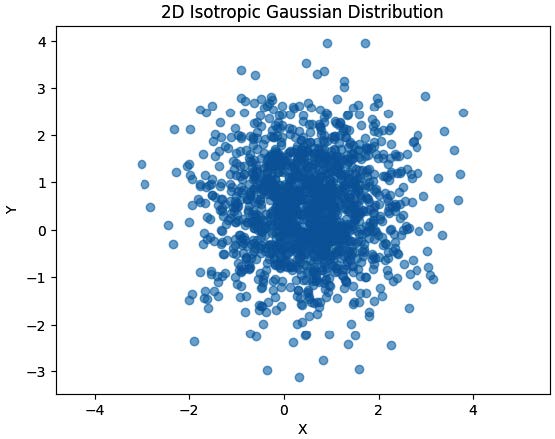
该图展示了代码如何通过仅 16 步高效地将一幅图像转化为接近各向同性、正态分布的噪声图像，正如图 2 的最后一幅图像所示。

一个更高效的正向扩散过程

如果我们使用链式过程在第 t 步计算一个噪声图像，则需要先计算从第 1 步到第 t-1 步的噪声图像，这样效率不高。我们可以利用一个称为重新参数化的技巧，将原始的链式过程转换为一步过程。以下是该技巧的具体实现：

假设我们有一个均值为 \mu、方差为 \sigma^2 的高斯分布 z：

z \sim \mathcal{N}(\mu, \sigma^2)

那么，我们可以将该分布重写为：

\epsilon \sim \mathcal{N}(0, 1)

z = \mu + \sigma \epsilon

这个技巧带来的好处是，我们现在可以通过一步计算在任意步骤生成图像，从而大大提升训练性能：

x_t = \sqrt{1-\beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon_{t-1}

现在，假设我们定义如下：

\alpha_t = 1 - \beta_t

那么：

\bar{\alpha}_t = \prod_{i=1}^{t} \alpha_i

这里没有任何“魔法”，定义 \alpha_t 和 \bar{\alpha}_t 只是为了简化计算，以便我们可以在第 t 步计算一个噪声图像，并使用以下公式从初始无噪声图像 x_0 生成 x_t：

x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon

那么 \alpha_t 和 \bar{\alpha}_t 看起来是什么样的呢？以下是一个简化示例（图 4）。

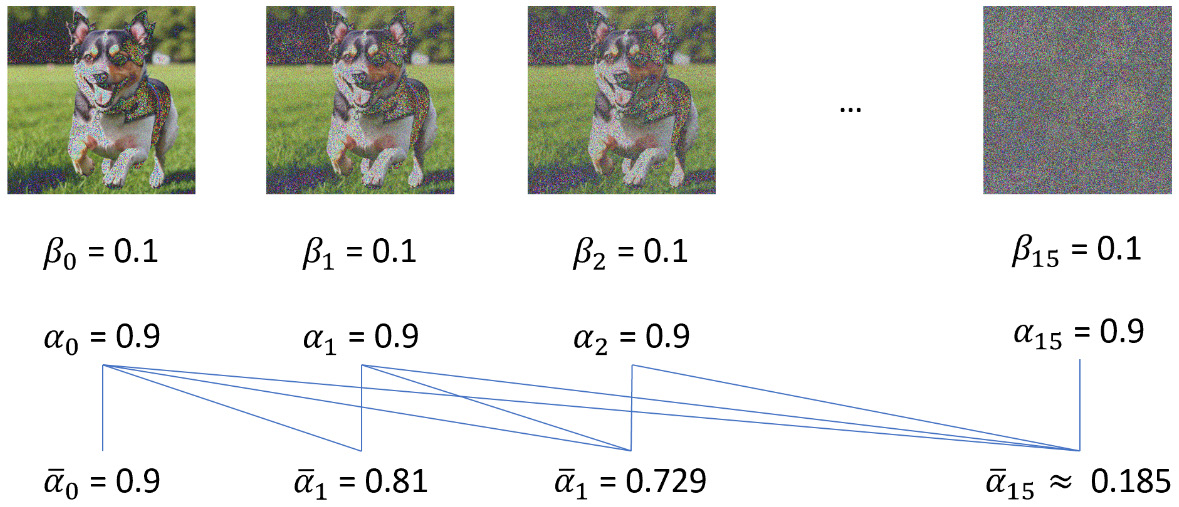
在图 4.4 中，我们有相同的 \alpha - 0.1 和 \beta - 0.9。现在，每当我们需要生成一个有噪声的图像 x_t 时，我们可以通过已知的数字快速计算 \bar{\alpha}_t；这些线条显示了用来计算 \bar{\alpha}_t 的数字。

以下代码可以在任何步骤生成有噪声的图像：

这段代码是之前展示的数学公式的实现。我在这里展示代码是为了帮助建立数学公式与实际实现之间的关联。如果你熟悉 Python，你可能会发现这段代码使得理解其中的细微差别变得更加容易。这段代码可以生成如图 5 所示的有噪声的图像。

现在，让我们思考如何利用神经网络恢复图像。

噪声到图像的训练过程

我们已经有了将噪声添加到图像中的解决方案，这被称为正向扩散，如图 6 所示。为了从噪声中恢复图像，或进行反向扩散，如图 6 所示，我们需要找到一种方法来实现反向步骤 p_\theta(x_{t-1} \mid x_t)。然而，这个步骤在没有额外帮助的情况下是不可计算的或难以求解的。

考虑到我们手中有最终的高斯噪声数据，以及所有这些噪声步骤数据。如果我们能训练一个神经网络来逆转这个过程呢？我们可以使用神经网络来提供噪声图像的均值和方差，然后从之前的图像数据中去除生成的噪声。通过这样做，我们应该能够使用这个步骤来表示 p_\theta(x_{t-1} \mid x_t)，从而恢复图像。

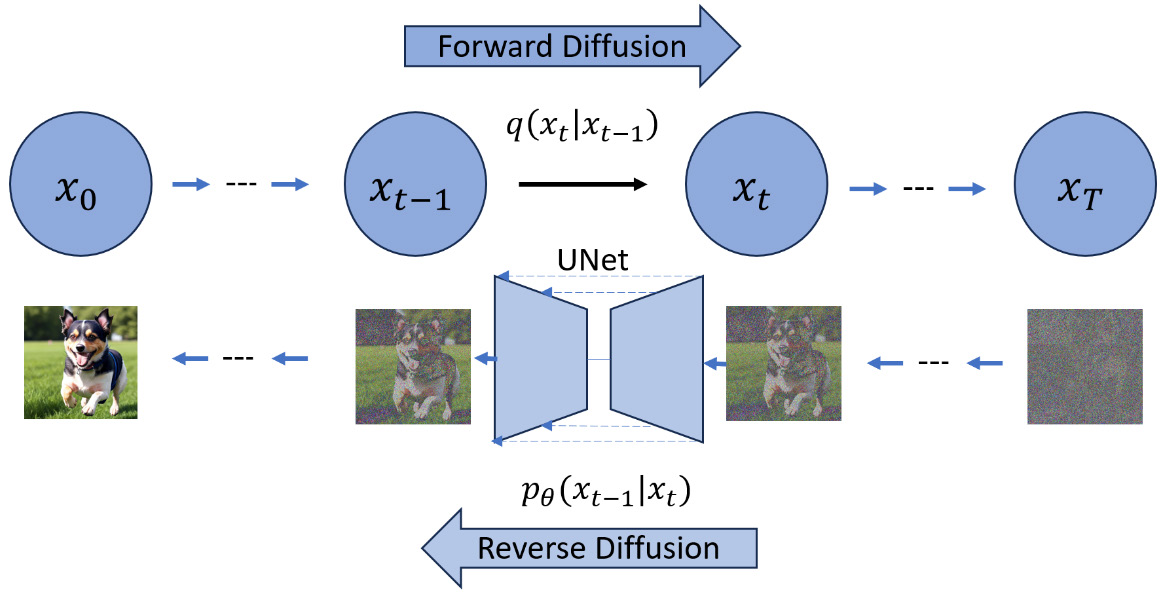
你可能会问，我们应该如何计算损失并更新权重。最终的图像 (x_T) 去除了之前添加的噪声，并将提供真实的标签数据。毕竟，我们可以在正向扩散过程中实时生成噪声数据。接下来，将其与神经网络（通常是 UNet）的输出数据进行比较。我们得到的损失数据可以用于计算梯度下降数据，并更新神经网络的权重。

DDPM 论文提供了一种简化的损失计算方法：

L_{simple}(\theta) := \mathbb{E}_{t, x_0, \epsilon} \left[ \left\| \epsilon - \epsilon_\theta \left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, t \right) \right\|^2 \right]

由于 x_t = \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon，我们可以进一步简化公式为：

L_{simple}(\theta) := \mathbb{E}_{t, x_0, \epsilon} \left[ \left\| \epsilon - \epsilon_\theta(x_t, t) \right\|^2 \right]

UNet 将接收一个加噪声的图像数据 x_t 和一个时间步数据 t 作为输入，如图 7 所示。为什么要将 t 作为输入？因为所有去噪过程共享相同的神经网络权重，输入的 t 将帮助训练一个考虑时间步的 UNet。

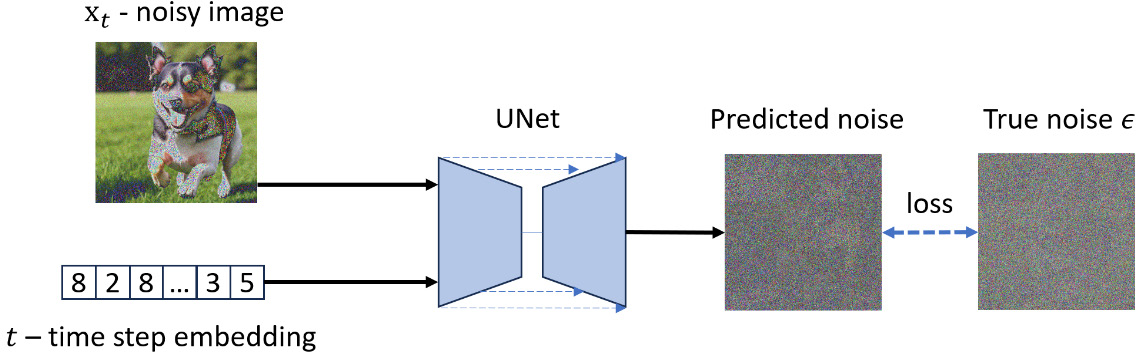
当我们说让我们训练一个神经网络来预测将从图像中去除的噪声分布，从而得到更清晰的图像时，神经网络到底在预测什么？在 DDPM 论文中，原始的扩散模型使用了一个固定的方差 \theta，并将高斯分布的均值 - \mu 作为唯一需要通过神经网络学习的参数。

在 PyTorch 的实现中，损失数据可以像这样计算：

噪声到图像的采样过程

以下是从模型采样图像的步骤，换句话说，这是从反向扩散过程生成图像的步骤：

1. 生成一个完整的高斯噪声，均值为 0，方差为 1：

x_T \sim \mathcal{N}(0, 1)

我们将使用这个噪声作为起始图像。

2. 从 t=T 到 t=1 进行循环。在每一步，如果 t>1，则生成另一个高斯噪声图像 z：

z \sim \mathcal{N}(0, 1)

如果 t=1，则执行以下操作：

z=0

然后，从 UNet 模型生成噪声，并从输入的噪声图像 x_t 中去除生成的噪声：

x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_\theta(x_t, t) \right) + \sqrt{1 - \alpha_t} \, z

如果我们看看上述公式，所有的 \alpha_t 和 \bar{\alpha_t} 是已知的数字，来源于 \beta_t。我们从 UNet 中唯一需要的就是 \epsilon_\theta(x_t, t)，即 UNet 生成的噪声，如图 8 所示。

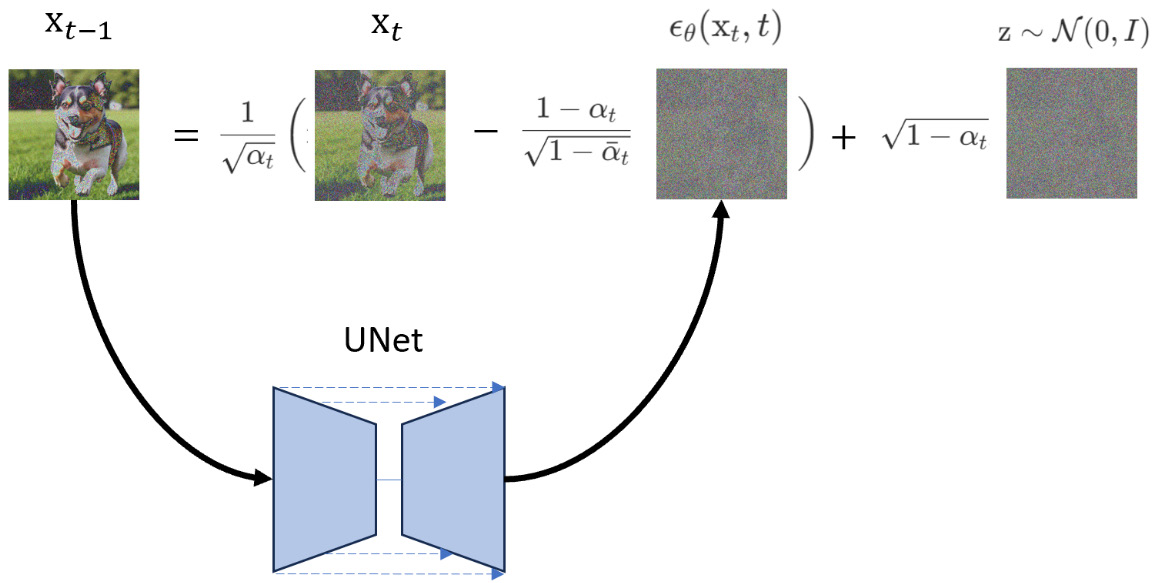
加入的 \sqrt{1 - \alpha_t} \, z 在这里看起来有点神秘。为什么要将其加入过程？原始论文并没有解释这部分噪声，但研究人员发现，去噪过程中加入的噪声会显著提高生成图像的质量！

3. 循环结束，返回最终生成的图像 x_0。

接下来，我们将讨论图像生成的引导。

理解分类器引导去噪

到目前为止，我们还没有讨论文本引导。在没有引导的情况下，图像生成过程仅使用随机高斯噪声作为输入，然后根据训练数据集随机生成一张图像。但我们希望有一个引导的图像生成过程；例如，输入“dog”来要求扩散模型生成一张包含“dog”的图像。

在2021年，OpenAI的Dhariwal和Nichol在他们的论文《Diffusion Models Beat GANs on Image Synthesis》中提出了分类器引导方法。

根据该方法，我们可以通过在训练阶段提供分类标签来实现分类器引导的去噪。除了图像或时间步嵌入，我们还提供文本描述的嵌入，如图 9 所示。

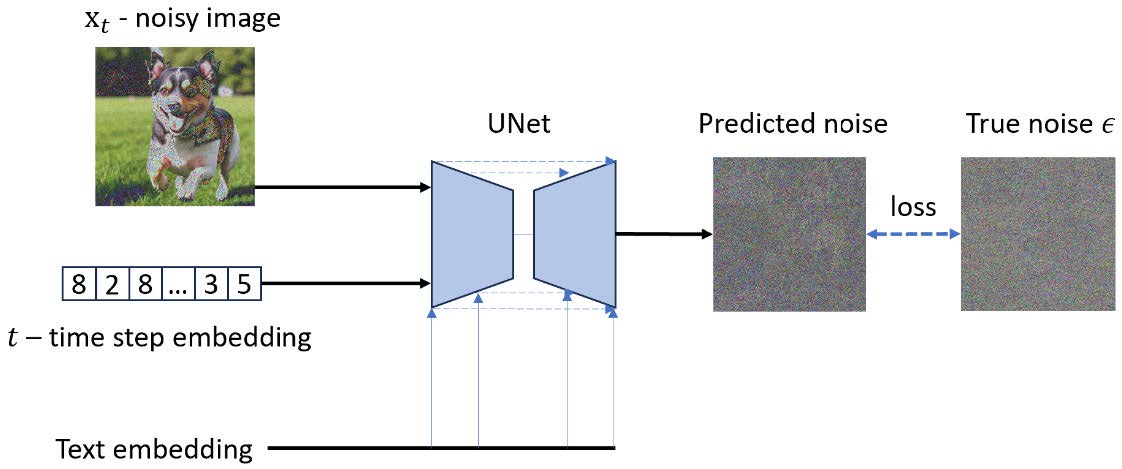
在图 7 中，有两个输入，而在图 9 中，增加了一个输入——文本嵌入。它是由 OpenAI 的 CLIP 模型生成的嵌入数据。我们将在下一章讨论更强大的 CLIP 模型引导的扩散模型。

总结

在这一章中，我们深入探讨了最初由 Jonathan Ho 等人提出的扩散模型的内部工作原理。我们了解了扩散模型的基础思想，并学习了正向扩散过程。我们还讨论了扩散模型训练和采样中的反向扩散过程，并探索了如何使文本引导的扩散模型成为可能。通过本章内容，我们旨在解释扩散模型的核心思想。如果你想自己实现一个扩散模型，我建议直接阅读原始的 DDPM 论文。

DDPM 扩散模型能够生成逼真的图像，但它的一个问题是性能。模型训练不仅慢，图像采样的速度也很慢。在下一章中，我们将讨论稳定扩散模型，它以一种巧妙的方式提高了速度。