1 上下文无关语法

1.1 上下文无关文法的定义

正规式可以来定义一些简单的语言，但是很多较复杂的语言不能用正规式表达。例如，正规式不能描述配对或嵌套的结构，具体的例子有，由配对括号构成的串的集合不能用正规式描述，语句的嵌套结构也不能用正规式描述。还有，很多重复串也不能用正规式表示，例如集合

\[ \{ wcw \mid w 是a和b的串 \} \]

不能用正规式描述。正规式只能表示给定结构的固定次数的重复或者不指定次数的重复。

本节定义描述功能比正规式更强的上下文无关文法，并介绍一些与分析有关的术语。

形式地说，一个上下文无关语法 \(G\) 是一个四元组 \( (V_T,V_N,S,P) \) ，其中：

（1） \(V_T\) 是一个非空有限集合，其元素称为终结符。在谈论编程语言的文法时，记号名是终结符的同义词。

（2） \(V_N\) 是一个非空有限集合，其元素称为非终结符，并有 \(V_T \cap V_N = \varnothing \)。在下面的例 1 中，\(expr\) 和 \(op\) 是非终结符。非终结符用来帮助定义由文法决定的语言，一个非终结符定义终结符串的一个集合。非终结符还在语言中强加了层次结构，这种层次结构对语法分析和翻译都是有用的。

（3） \(S\) 是一个非终结符，称为开始符号，它定义的终结符串集就是文法定义的语言。

（4） \(P\) 是产生式的有限集合，每个产生式的形式是 \(A \rightarrow \alpha \)，其中 \( A \in V_N, \alpha \in {(V_T \cup V_N)}^*\)。开始符号至少出现在某个产生式的左部。产生式指明了终结符和非终结符组成串的方式。

例1    文法 \( (\{id,+,*,-,(,)\},\ \{expr,op\},\ expr,\ P) \)，定义了包含加、乘和一元减的算术表达式。\(P\) 由下列产生式组成：

\( expr \rightarrow expr \ op \ expr \)
\( expr \rightarrow (expr) \)
\( expr \rightarrow -expr \)
\( expr \rightarrow id \)
\( op \rightarrow + \)
\( op \rightarrow * \)

例2    使用这些简写，例 1 的文法可以重新表示如下：

\( E \rightarrow EAE \mid (E) \mid -E \mid id \ \ (1.1)\)
\( A \rightarrow + \mid * \)

其中，\(E\) 和 \(A\) 都是非终结符，\(E\) 是开始符号，其余符号都是终结符。

1.2 二义性

有些文法的一些句子存在不止一颗分析树，或者说这些句子存在不止一种最左（最右）推导。

例3    考虑算术表达式文法 (1.1) ，句子 \(id * id + id\) 两种不同的最左推导如下：

\( E \Rightarrow E * E\)
\( \Rightarrow id * E\)
\( \Rightarrow id * E + E\)
\( \Rightarrow id * id + E\)
\( \Rightarrow id * id + id\)

\( E \Rightarrow E + E\)
\( \Rightarrow E * E + E\)
\( \Rightarrow id * E + E\)
\( \Rightarrow id * id + E\)
\( \Rightarrow id * id + id\)

因而有两棵不同的分析树，见图 1。

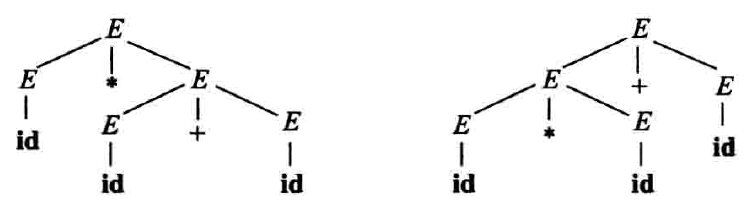
注意，图 1 右边的分析树反映了 \(+\) 和 \(*\) 通常的优先关系，而图 1 左边的分析树则不是。也就是，习惯上 \(*\) 的优先级高于 \(+\)，因而表达式 \(a*b+c\) 看成 \((a*b)+c\)，而不是 \(a*(b+c)\)。

一个文法，如果存在某个句子有不止一棵分析树与之对应，那么称这个文法是二义的。也可以这么说，二义文法是至少存在一个句子有不止一个最左（最右）推导的文法。有些类型的分析器，它希望处理的文法是无二义性的，否则它不能唯一确定对某个句子应该选择哪颗分析树。出于某些需要，也可以构造允许二义文法的分析器，不过这样的文法要附带消除二义性的规则，以便分析器扔掉不希望的分析树，为每个句子只留一棵分析树。

注意，文法二义并不代表语言一定是二义的。只有当产生一个语言的所有文法都是二义时，这个语言才是二义的。

2 语言和文法

2.1 适当的表达式文法

1 节构造的表达式文法有二义性，一个句子的不同分析树体现了不同的算符优先关系和算符结合性。下面构造非二义的有 \(+\) 和 \(*\) 运算的表达式文法，该文法和通常的算符优先关系和算符结合性相对应。

设置两个非终结符 \(expr\) 和 \(term\) （\(expr\) 是开始符号），用以表示不同层次的表达式和子表达式，再用非终结符 \(factor\) 来产生表达式的基本单位。基本单位有 \(id\) 和外加括号的表达式，即

\(factor \rightarrow id \mid (expr)\)

然后考虑二元算符 \(*\) ，它有较高的优先级，又是左结合的算符，因而产生式如下：

\(term \rightarrow term * factor \mid factor\)

同样地，\(expr\) 产生由加法算符隔开的、左结合的 \(term\) 表，其产生式如下：

\(expr \rightarrow expr + term \mid term\)

2.2 消除左递归

一个文法是左递归，如果它有非终结符 \(A\)，对某个串 \(\alpha\)，存在推导 \(A {\Rightarrow}^+ A\alpha\)。自上而下的分析方法不能用于左递归文法，因此需要消除左递归。由形式为 \(A \rightarrow A\alpha\) 的产生式引发的左递归称为直接左递归。

左递归产生式 \(A \rightarrow A\alpha \mid \beta \) 可以用非左递归的

\(A \rightarrow \beta{A}^{\prime} \)
\({A}^{\prime} \rightarrow \alpha{A}^{\prime} \mid \varepsilon \)

来代替，它们没有改变从 \(A\) 推导出的串集。

例4    考虑下面的算术表达文法：

\(E \rightarrow E + T \mid T\)
\(T \rightarrow T * F \mid F\)
\(F \rightarrow (E) \mid id \)

消除 \(E\) 和 \(T\) 的直接左递归，可以得到

\(E \rightarrow T{E}^{\prime}\)
\({E}^{\prime} \rightarrow +T{E}^{\prime} \mid \varepsilon \)
\(T \rightarrow F{T}^{\prime}\)
\({T}^{\prime} \rightarrow *F{T}^{\prime} \mid \varepsilon \)
\(F \rightarrow (E) \mid id \)

不管有多少 \(A\) 产生式，都可以用下面的技术消除直接左递归。首先把 \(A\) 产生式组合在一起：

\(A \rightarrow A{\alpha}_1 \mid A{\alpha}_2 \mid \cdots \mid A{\alpha}_m \mid {\beta}_1 \mid {\beta}_2 \mid \cdots \mid {\beta}_n \)

其中 \({\beta}_i\) 都不以 \(A\) 开始，\({\alpha}_i\) 都非空，然后用

\(A \rightarrow {\beta}_{1}{A}^{\prime} \mid {\beta}_{2}{A}^{\prime} \mid \cdots \mid {\beta}_{n}{A}^{\prime} \)
\({A}^{\prime} \rightarrow {\alpha}_{1}{A}^{\prime} \mid {\alpha}_{2}{A}^{\prime} \mid \cdots \mid {\alpha}_{m}{A}^{\prime} \mid \varepsilon \)

代替 \(A\) 产生式。这些产生式和前面的产生式产生一样的串集，但是不再有左递归。这个过程可删除直接左递归，但不能消除两步或多步推导形成的左递归。例如，考虑文法

\(S \rightarrow Aa \mid b \)
\(A \rightarrow Sd \mid \varepsilon \)

其中非终结符 \(S\) 是左递归的，因为 \( S \Rightarrow Aa \Rightarrow Sda\)，但它不是直接左递归的。用 \(S\) 产生式代换 \( A \rightarrow Sd \) 中的 \(S\)，可以得到下面的文法：

\(S \rightarrow Aa \mid b \)
\(A \rightarrow Aad \mid bd \mid \varepsilon \)

删除其中的直接左递归，得到如下的文法：

\(S \rightarrow Aa \mid b \)
\(A \rightarrow bdA^{\prime} \mid A^{\prime} \)
\(A^{\prime} \rightarrow adA^{\prime} \mid \varepsilon \)

由此可见，写一个删除文法左递归的算法并不是件困难的事情。

2.3 提左因子

提取左因子也是一种文法变换，它用于产生适合于自上而下分析的文法。在自上而下的分析中，当不清楚应该用非终结符 \(A\) 的哪个选项来替换它时，可以通过重写 \(A\) 产生式来推迟这种决定，推迟到看见足够的输入，能帮助正确决定所需选择为止。

例如，条件语句有两个产生式：

\( stmt \rightarrow \textbf{if}\ expr\ \textbf{then}\ stmt\ \textbf{else}\ stmt \)
\( \mid\ \textbf{if}\ expr\ \textbf{then}\ stmt\)

当看见输入记号 if 时，不能马上确定用哪个产生式来扩展 \(stmt\) 。

一般来说，如果 \(A \rightarrow \alpha\beta_1 \mid \alpha\beta_2\) 是两个产生式，输入串的前缀是从 \(\alpha\) 推导出的非空串时，则不知道是用 \(\alpha\beta_1\) 还是用 \(\alpha\beta_2\) 来扩展 \(A\)。但是可以通过先扩展 \(A\) 到 \(\alpha A^{\prime}\) 来推迟这个决定。然后，看完了从 \(\alpha\) 推出的输入后，再扩展 \(A^{\prime}\) 到 \(\beta_1\) 或 \(\beta_2\)。这就是提左因子，原来的产生式成为：

\(A \rightarrow \alpha A^{\prime}\)
\(A^{\prime} \rightarrow \beta_1 \mid \beta_2\)

3. 自上而下分析

3.1 LL(1) 文法

为构造不带回溯的自上而下分析算法，首先要消除文法的左递归，并找出避免回溯的充分必要条件。消除左递归的方法已介绍，下面讨论如何避免回溯。

对文法的任何非终结符，当要用它去匹配输入串时，如果能够根据所面临的输入符号准确地指派它的一个选择去执行任务，那么就肯定能消除回溯。这个“准确”是指：若此选择匹配成功，那么这种匹配绝不是虚假的；若此选择无法完成匹配任务，则任何其他的选择也肯定无法完成。

在讨论不得回溯的前提对文法有什么限制之前，先定义两个和文法有关的函数。一个文法的符号串 \(\alpha\) 的开始符号集合 \(FIRST(\alpha)\) 是

\( FIRST(\alpha) = \{ a \mid \alpha {\Rightarrow}^{*} a \cdots ,a \in V_T\} \)

特别是，\( \alpha {\Rightarrow}^{*} \varepsilon \) 时，规定 \( \varepsilon \in FIRST(\alpha) \)。如果对 \(A\) 的任何两个不同的选择 \(\alpha_i\) 和 \(\alpha_j\) ，有

\( FIRST(\alpha_i) \cap FIRST(\alpha_j) = \varnothing \)

那么，当要求 \(A\) 匹配输入串时，\(A\) 就能根据它所面临的第一个输入符号 \(a\) ，准确地指派某一个选择前去执行任务。这个选择就是满足 \(a \in FIRST(\alpha)\) 的那个 \(\alpha\)。

已经介绍过，用提取左因子的办法，可以把文法改造成对任何非终结符 \(A\)，\(A\) 的所有选择的开始集合两两不相交。

如何 \(\varepsilon\) 属于 \(A\) 的某个选择的开始符号集合，那么问题就比较复杂，需要定义文法非终结符的后继符号集合后才能解释。非终结符 \(A\) 的后继符号集合 \(FOLLOW(A)\) 是所有在句型中可以直接出现在 \(A\) 后面的终结符的集合，也就是

\( FOLLOW(A) = \{ a \mid S {\Rightarrow}^{*} \cdots Aa \cdots,a \in V_T\} \)

如果 \(A\) 是某个句型的最右符号，那么 \($\) 也属于 \(FOLLOW(A)\)。

例4    考虑如下的文法：

\( E \rightarrow TE^{\prime} \)
\( E^{\prime} \rightarrow +TE^{\prime} \mid \varepsilon \)
\( T \rightarrow FT^{\prime} \)
\( T^{\prime} \rightarrow *FT^{\prime} \mid \varepsilon \)
\( F \rightarrow (E) \mid id \)

那么

\( FIRST(E)=FIRST(T)=FIRST(F)= \{(,id\} \)
\( FIRST(E^{\prime})= \{+,\varepsilon\}\)
\( FIRST(T^{\prime})= \{*,\varepsilon\}\)

有了上面这些 \(FIRST\) 集合后，就不难计算各产生式右部的 \(FIRST\) 集合了。

再看 \(FOLLOW\) 集合。这里要注意的是，如果有产生式 \(A \rightarrow \alpha B \) 或 \(A \rightarrow \alpha B \beta \) 且 \( \beta \Rightarrow^{*} \varepsilon \)，那么 \(FOLLOW(A)\) 的一切元素都要加入 \(FOLLOW(B)\) 中。

\( FOLLOW(E) = FOLLOW(E^{\prime}) = \{),$\} \)
\( FOLLOW(T) = FOLLOW(T^{\prime}) = \{+,),$\} \)
\( FOLLOW(F) = \{+,*,),$\} \)

设计一个算法来计算开始符号集合和后继符号集合是件容易的事情。

下面回到 \(\varepsilon\) 属于 \(A\) 的某个选择 \(\beta\) 的开始符号集合这个问题。如果 \(a\) 属于 \(A\) 的另一个选择 \(\alpha\) 的开始符号集合，并且 \(a\) 属于 \(FOLLOW(A)\) ，那么面临 \(a\) 为 \(A\) 做选择时，选择 \(\alpha\) 和 \(\beta\) 都是有理由的，其中选择后者的理由是让 \(\beta\) 推出空串，把这个 \(a\) 看成是 \(A\) 的后继符号。

这样，要想不出回溯，需要文法的任何两个产生式 \(A \rightarrow \alpha \mid \beta \) 都满足下面两个条件：

\( FIRST(\alpha) \cap FIRST(\beta) = \varnothing \)
若 \(\beta {\Rightarrow}^{*} \varepsilon \) ，那么 \( FIRST(\alpha) \cap FOLLOW(A) = \varnothing \)

把满足着两个条件的文法成为LL(1)文法，其中的第一个“L”代表从左向右的扫描输入，第二个“L”表示产生最左推导，“1”代表在决定分析器的每步动作时需要向前查看下一输入符号（即输入指针所指向的符号）。除了没了公共左因子外，LL(1)文法还有一些明显的性质，它不是二义的，也不含左递归。

构造预测分析表

下面的算法为文法 \(G\) 构造预测分析表 \(M[A,a]\)，其中 \(A\) 是非终结符，\(a\) 是终结符或 \($\)。这个算法的思想如下：如果 \(A \rightarrow \alpha \) 是产生式且 \(a\) 在 \(FIRST(\alpha)\) 中，那么在当前输入符号为 \(a\) 时，分析器选择用 \(\alpha\) 展开 \(A\)。唯一的复杂情况是 \(\alpha {\Rightarrow}^{*} \varepsilon \) ，在这种情况下，如果当前输入符号（包括\($\)）在 \(FOLLOW(A)\) 中，仍应用 \(\alpha\) 展开 \(A\)。