数据 - 统一变量

2021-12-5

[已归档]OpenGL入门

这一篇文章开始介绍统一变量，也有些地方翻译成一致变量。这个变量有点全局变量的感觉，如果在多个着色器阶段声明同一统一变量，那么每个阶段都会涉及该统一变量相同的值。一般使用统一变量来存储如模型-视图、投影矩阵等变量。

创建一个统一变量也很简单，只需要在变量声明前加上 uniform 关键字，如：

  • uniform float fTime;

设置统一变量使用 glUniform*() 这一系列函数，比如设置

  • uniform vec4 vColor;

我们可以使用 glUniform4fv() 函数：

  • GLfloat vColor[4] = { 1.0f, 1.0f, 1.0f, 1.0f };
  • glUniform4fv(iColorLocation, 1, vColor);

其定义为：

  • void glUniform4fv(GLint location, GLsizei count, const GLfloat *value);

其中的 count 和 value 参数都好理解，主要需要说明一下 location 参数。在程序对象中使用位置来指代定位某一统一变量，即这边的 location 参数需要指定想要修改的统一变量的位置。

可以使用 glGetUniformLocation() 函数来获取分配的位置：

  • GLint glGetUniformLocation(GLuint program, const GLchar *name);

比如，以上我需要获取 vColor 统一变量的位置：

  • GLint iColorLocation = glGetUniformLocation(myProgram, "vColor");

如果我们使用位置限定符，则 OpenGL 会尝试将指定的位置分配给统一变量，就不用再调用 glGetUniformLocation() 来获取了。这边说的“尝试”的意思的，指定可能会出错，比如和其他指定的位置有冲突。

  • layout(location = 17) uniform vec4 vColor;

使用统一变量转换几何图形

以上学习的 glGetUniformLocation() 和 glUniform*() 已经够我们实现内容了。在这一节中，我们来使用统一变量来实现旋转立方体的例子。

清单 5.22 的内容我们比较熟悉，所做的事情就是将构成正方体的顶点数据写入顶点数组对象。正方体有 6 个面，每个面由 2 个三角形构成，所以 vertex_positions 数组占了大多数篇幅。

原书清单 5.22 建立立方体的几何结构
  • // First create and bind a vertex array object
  • glGenVertexArrays(1, &vao);
  • glBindVertexArray(vao);
  •  
  • static const GLfloat vertex_positions[] =
  • {
  •     -0.25f,  0.25f, -0.25f,
  •     -0.25f, -0.25f, -0.25f,
  •      0.25f, -0.25f, -0.25f,
  •  
  •      0.25f, -0.25f, -0.25f,
  •      0.25f,  0.25f, -0.25f,
  •     -0.25f,  0.25f, -0.25f,
  •  
  •      0.25f, -0.25f, -0.25f,
  •      0.25f, -0.25f,  0.25f,
  •      0.25f,  0.25f, -0.25f,
  •  
  •      0.25f, -0.25f,  0.25f,
  •      0.25f,  0.25f,  0.25f,
  •      0.25f,  0.25f, -0.25f,
  •  
  •      0.25f, -0.25f,  0.25f,
  •     -0.25f, -0.25f,  0.25f,
  •      0.25f,  0.25f,  0.25f,
  •  
  •     -0.25f, -0.25f,  0.25f,
  •     -0.25f,  0.25f,  0.25f,
  •      0.25f,  0.25f,  0.25f,
  •  
  •     -0.25f, -0.25f,  0.25f,
  •     -0.25f, -0.25f, -0.25f,
  •     -0.25f,  0.25f,  0.25f,
  •  
  •     -0.25f, -0.25f, -0.25f,
  •     -0.25f,  0.25f, -0.25f,
  •     -0.25f,  0.25f,  0.25f,
  •  
  •     -0.25f, -0.25f,  0.25f,
  •      0.25f, -0.25f,  0.25f,
  •      0.25f, -0.25f, -0.25f,
  •  
  •      0.25f, -0.25f, -0.25f,
  •     -0.25f, -0.25f, -0.25f,
  •     -0.25f, -0.25f,  0.25f,
  •  
  •     -0.25f,  0.25f, -0.25f,
  •      0.25f,  0.25f, -0.25f,
  •      0.25f,  0.25f,  0.25f,
  •  
  •      0.25f,  0.25f,  0.25f,
  •     -0.25f,  0.25f,  0.25f,
  •     -0.25f,  0.25f, -0.25f
  • };
  •  
  • // Now generate some data and put it in a buffer object
  • glGenBuffers(1, &buffer);
  • glBindBuffer(GL_ARRAY_BUFFER, buffer);
  • glBufferData(GL_ARRAY_BUFFER,
  •              sizeof(vertex_positions),
  •              vertex_positions,
  •              GL_STATIC_DRAW);
  • // Set up our vertex attribute
  • glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, NULL);
  • glEnableVertexAttribArray(0);

紧接着我们实现清单 5.26 所示的顶点着色器，其中定义了一个平移矩阵和透视矩阵。这些矩阵都通过统一变量进行存储。颜色数据我们通过接口块定义，颜色和位置相关。

原书清单 5.26 旋转立方体的顶点着色器
  • #version 450 core
  •  
  • in vec4 position;
  •  
  • out VS_OUT
  • {
  •     vec4 color;
  • } vs_out;
  •  
  • uniform mat4 mv_matrix;
  • uniform mat4 proj_matrix;
  •  
  • void main(void)
  • {
  •     gl_Position = proj_matrix * mv_matrix * position;
  •     vs_out.color = position * 2.0 + vec4(0.5, 0.5, 0.5, 0.0);
  • }

再定义如清单 5.27 所示的片段着色器，比较简单就不再赘述了。

原书清单 5.27 旋转立方体的片段着色器
  • #version 450 core
  •  
  • out vec4 color;
  •  
  • in VS_OUT
  • {
  •     vec4 color;
  • } fs_in;
  •  
  • void main(void)
  • {
  •     color = fs_in.color;
  • }

现在终于到了我们学习的 glUniformMatrix4fv() 函数的用武之地了。以下，我们将书上的两份代码合在一块，因为都在 render 函数中进行。其实现的功能为逐帧改变立方体的平移（旋转）矩阵。

原书清单 5.23 为旋转立方体构建模型视图矩阵
原书清单 5.27 旋转立方体的渲染循环
  • // Clear the framebuffer with dark green
  • glClearBufferfv(GL_COLOR, 0, sb7::color::Green);
  •  
  • // Activate our program
  • glUseProgram(program);
  •  
  • float f = currentTime * (float)M_PI * 0.1f;
  • vmath::mat4 mv_matrix =
  •     vmath::translate(0.0f, 0.0f, -4.0f) *
  •     vmath::translate(sinf(2.1f * f) * 0.5f,
  •                      cosf(1.7f * f) * 0.5f,
  •                      sinf(1.3f * f) * cosf(1.5f * f) * 2.0f) *
  •     vmath::rotate((float)currentTime * 45.0f, 0.0f, 1.0f, 0.0f) *
  •     vmath::rotate((float)currentTime * 81.0f, 1.0f, 0.0f, 0.0f);
  •  
  • // Set the model-view and projection matrices
  • glUniformMatrix4fv(mv_location, 1, GL_FALSE, mv_matrix);
  • glUniformMatrix4fv(proj_location, 1, GL_FALSE, proj_matrix);
  • glDrawArrays(GL_TRIANGLES, 0, 36);

透视矩阵和窗体相关，如清单 5.24 所示，我们在窗体变化的时候更新透视矩阵。

原书清单 5.24 更新旋转立方体的投影矩阵
  • void onResize(int w, int h)
  • {
  •     sb7::application::onResize(w, h);
  •  
  •     aspect = (float)info.windowWidth / (float)info.windowHeight;
  •     proj_matrix = vmath::perspective(50.0f,
  •                                      aspect,
  •                                      0.1f,
  •                                      1000.0f);
  • }

书中示例缺漏太多

单单照着书上给的片段运行会有问题，还需要注意许多小的地方。总体参照配套例子—— spinnycube 即可。

● 透视矩阵需要在 startup 里初始化一下，因为刚运行的时候调用不到 onResize。

● 当窗体变化时，需要调用 glViewport() 调整视口。

● glEnable(GL_CULL_FACE) 启用背面剔除；此例中 glFrontFace(GL_CW) 设置顺时针为正面。不指定这些，会有一半的面是透明的。

● 统一变量的位置在 startup 里通过 glGetUniformLocation() 进行获取。

参照配套例子 spinnycube 进行排查。

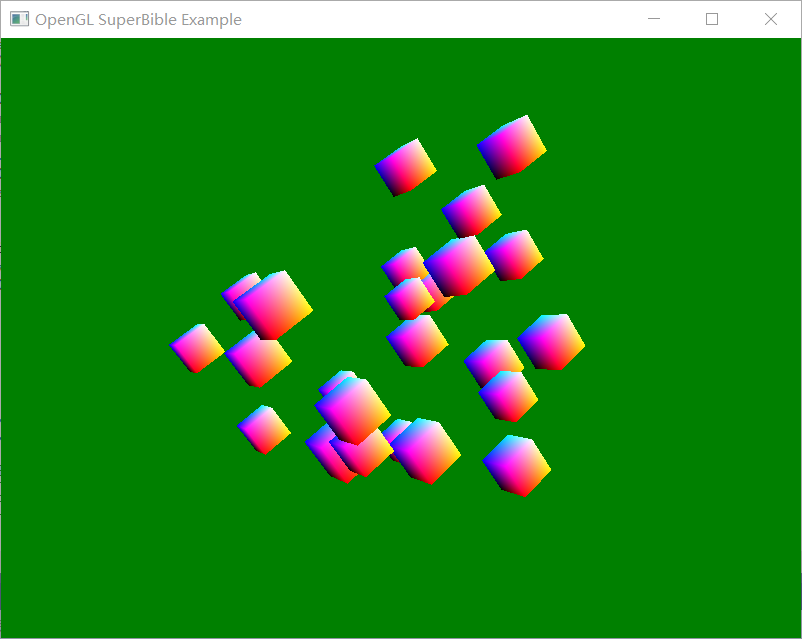
就这样，我们的旋转立方体终于实现了：

例1 旋转的立方体

如清单 5.28 所示，大同小异，我们可以画多个立方体，针对每个都改变其变换矩阵。

原书清单 5.28 旋转立方体的渲染循环
  • // Clear the framebuffer with dark green and clear
  • // the depth buffer to 1.0
  • glClearBufferfv(GL_COLOR, 0, sb7::color::Green);
  • glClearBufferfi(GL_DEPTH_STENCIL, 0, 1.0f, 0);
  •  
  • // Activate our program
  • glUseProgram(program);
  •  
  • // Set the model-view and projection matrices
  • glUniformMatrix4fv(proj_location, 1, GL_FALSE, proj_matrix);
  •  
  • // Draw 24 cubes
  • for (i = 0; i < 24; i++)
  • {
  •     // Calculate a new model-view matrix for each one
  •     float f = (float)i + (float)currentTime * 0.3f;
  •     vmath::mat4 mv_matrix =
  •         vmath::translate(0.0f, 0.0f, -10.0f) *
  •         vmath::rotate((float)currentTime * 45.0f, 0.0f, 1.0f, 0.0f) *
  •         vmath::rotate((float)currentTime * 21.0f, 1.0f, 0.0f, 0.0f) *
  •         vmath::translate(sinf(2.1f * f) * 2.0f,
  •             cosf(1.7f * f) * 2.0f,
  •             sinf(1.3f * f) * cosf(1.5f * f) * 2.0f);
  •  
  •     // Update the uniform
  •     glUniformMatrix4fv(mv_location, 1, GL_FALSE, mv_matrix);
  •     // Draw - notice that we haven't updated the projection matrix
  •     glDrawArrays(GL_TRIANGLES, 0, 36);
  • }
例2 多个立方体

一致区块

在之前我们已经了解过接口块，它是对输入输出数据的封装。自然的，也会有对统一变量的封装，它叫做一致区块。

一致区块按如下进行声明，此处我们紧接上面的例子。不仅包含了原本用到的两个矩阵，同时塞进了一些暂时用不到的数据，假装我们有很多数据需要使用一致区块到😜 同时也便于展示后续的“内存布局”。

  • uniform TransformBlock
  • {
  •     float scale;
  •     vec3 translation;
  •     float rotation[3];
  •     mat4 mv_matrix;
  •     mat4 proj_matrix;
  • } transform;

使用的方法也和接口块一样：

  • gl_Position = transform.proj_matrix * transform.mv_matrix * position;

着色器中一致区块的各个变量布局也是依据 OpenGL 编译器的。这和 C 里面的结构体一样，内存的布局并不会是你想象的那样，会有一些对齐的规则。书中建议我们使用 layout(std140) 限定符进行修饰，这样变量的布局就满足标准，可以预知，从而方便我们直接对一致区块的缓冲进行赋值。

但是，我后续就不记录 layout(std140) 限定符的相关内容了，因为我实验过程中踩坑了，暂时觉得不好用。我觉得查询的方式更加明明白白，心里有底。后续就介绍如何查询获取一致区块的布局信息。

如清单 5.14 所示，首先按成员的名称通过 glGetUniformIndices() 函数获取其对应的索引，后续查询都是按照索引进行的。

原书清单 5.14 改 获取一致区块成员的索引
  • static const GLchar* uniformNames[5] =
  • {
  •     "TransformBlock.scale",
  •     "TransformBlock.translation",
  •     "TransformBlock.rotation",
  •     "TransformBlock.mv_matrix",
  •     "TransformBlock.proj_matrix"
  • };
  • GLuint uniformIndices[5];
  •  
  • glGetUniformIndices(program, 5, uniformNames, uniformIndices);

接着就可以根据索引通过 glGetActiveUniformsiv() 函数获取各个成员的信息。清单 5.15 中获取了变量偏移、数组步长、矩阵步长这些信息。这些信息已经足够我们对当前的变量进行赋值。

原书清单 5.15 改 获取一致区块成员的信息
  • GLintuniformOffsets[5];
  • GLintarrayStrides[5];
  • GLintmatrixStrides[5];
  • glGetActiveUniformsiv(program,5,uniformIndices,GL_UNIFORM_OFFSET,uniformOffsets);
  • glGetActiveUniformsiv(program,5,uniformIndices,GL_UNIFORM_ARRAY_STRIDE,arrayStrides);
  • glGetActiveUniformsiv(program,5,uniformIndices,GL_UNIFORM_MATRIX_STRIDE,matrixStrides);

如图 2 所示，一致区块的缓冲操作和顶点数组对象类似，还涉及到一个绑定点。即一致区块不仅要和缓冲对象建立联系，还需要绑定到某一绑定点，不知道为什么要这么做。

图 2 绑定缓存与一致区块到绑定点

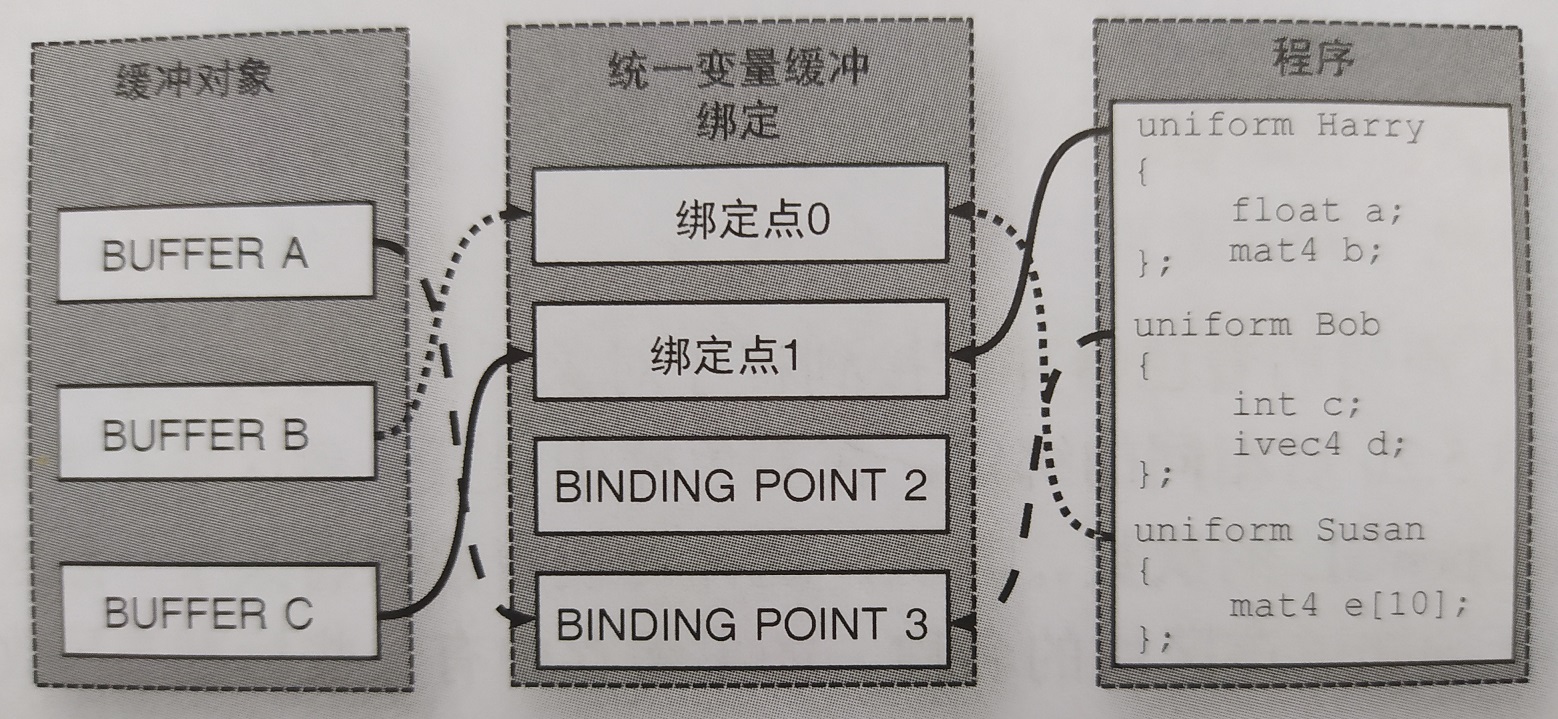
图 2 中最右边的程序一列，使用一致区块的索引进行定位，可使用 glGetUniformBlockIndex() 进行查询，特别指定一致区块的名称 uniformBlockName 即可：

  • GLuint glGetUniformBlockIndex(GLuint program,
  •                               const GLchar *uniformBlockName);

一致区块绑定到绑定点，需要调用 glUniformBlockBinding() 函数：

  • void glUniformBlockBinding(GLuint program,
  •                            GLuint uniformBlockIndex,
  •                            GLuint uniformBlockBinding);

一致区块绑定到缓冲，需要调用 glBindBufferBase() 函数：

  • void glBindBufferBase(GLenum target,
  •                       GLuint index,
  •                       GLuint buffer);

了解了以上相关函数，我们可以使用一致区块改造我们之前实现的旋转正方体。首先申请缓冲还是老样子，注意样例中的例子只是估摸了一个够用的大小，应该是有确切获取大小的方式。接着就是调用上面介绍的函数 —— glGetUniformBlockIndex() 和 glUniformBlockBinding()。

  • glCreateBuffers(1, &buffer);
  • glNamedBufferStorage(buffer, 0x200, NULL, GL_MAP_WRITE_BIT);
  •  
  • GLuint index = glGetUniformBlockIndex(program, "TransformBlock");
  • glBindBufferBase(GL_UNIFORM_BUFFER, index, buffer);
  • glUniformBlockBinding(program, index, 0);

之后操作也是缓冲上学过的操作，先映射到 CPU 可以操作的地址空间，最后也不要忘记释放映射。根据之前获取的偏移和步长信息就能写已经和一致区块绑定的缓冲。这边查看到步长是没有额外对齐的，就特别写了两种方式，以强调步长信息的作用。

  • char* ptr = (char*)glMapNamedBuffer(buffer, GL_WRITE_ONLY);
  •  
  • char* mvMatrixPtr = ptr + uniformOffsets[3];
  • for (i = 0; i < 4; i++)
  • {
  •     memcpy(mvMatrixPtr, &mv_matrix[i], 4 * sizeof(mv_matrix[0][0]));
  •     mvMatrixPtr += matrixStrides[3];
  • }
  •  
  • memcpy(ptr + uniformOffsets[4], &proj_matrix, sizeof(proj_matrix));
  •  
  • glUnmapNamedBuffer(buffer);

总结

整体上统一变量的实验还算简单有趣。有点枯燥待琢磨的是一致区块的介绍，目前了解下来需要注意变量的分布。

同时文章开头就说统一变量是有点全局变量的意思，就免不了“冲突”。我看文章有一部分介绍 OpenGL 的同步操作，先不做了解，后续用到再看。